解读FM合成器『5』--FM理论基础

解读FM合成器『5』--FM理论基础
前面我们已经讲了一些使用FM7制作FM音色的例子和方法了,要想制作属于你的FM音色,起码要了解一些FM合成的理论,这也许有些枯燥,但在有了FM7的兴趣下,咱们硬着头皮也要学完啊。
开始!(如果数学不好看不懂公式别怕,看文字就好了,祝你成功)
看下面的两个式子:
式子1:
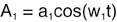
式子2:
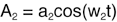
他们都是正弦形式的波形,他们的瞬时振幅A与他们的最大振幅a、频率w、时间t都有关系。式子1和式子2分别有不同的最大振幅a1、a2,频率w1、w2,所以他们的瞬时振幅也不同,分别是A1和A2。
之后我们使用第二个波形的振幅(也就是第二个式子代表的波形)来调制第一个波形的振幅(式子1),可以写成下面的式子3:
式子3:
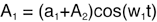
如果用第二个波形的振幅来调制第一个波形的频率会怎么样?就变成了式子4那样。
式子4:
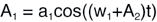
仔细对比式子3和式子4,差不多一样,只是A2变了个位置,式子3里A2用来调制式子1的振幅,这叫做振幅调制,而式子4里A2用来调制式子1的频率,这就是频率调制了。
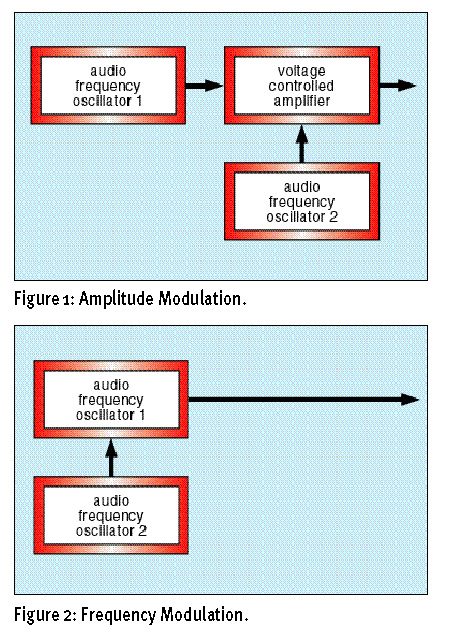
如果用图来表示,就是下图那样,式子1发出的波形可以看作是一个振荡器(audio Frequency oscillator)发出的波形,上面的图(Figure1)用式子2来调制式子1的振幅(振幅可以看作是一个压控放大器voltage controlled amplifier)这就是振幅调制,而下面的图(Figure2)表示式子2直接调制式子1的频率,这就是频率调制了。
之后我们将式子4里面的A2带成A2自己的形式,于是得到式子5(请仔细看,和式子4表示的一样):
式子5:
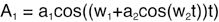
FM简单说来就是非常快的震颤
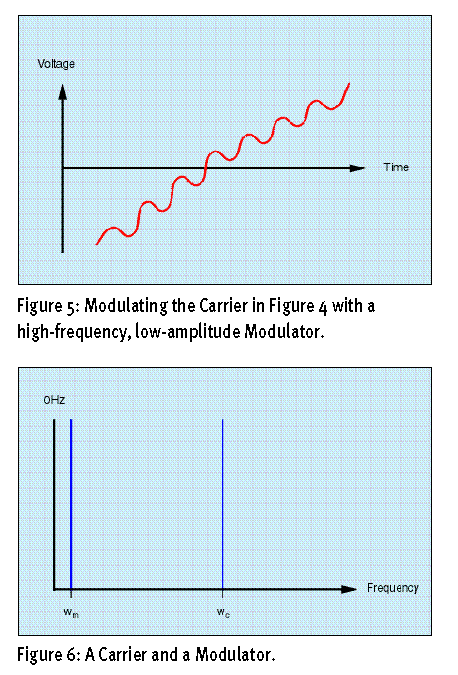
看下图(Figure3),表示了一个被调制源(就是FM7里面的调制器)震来颤去的波形(FM7里的载波器,前面咱们讲过的,谢天谢地你还记得),仔细看红色的波形(一定要仔细看),比较稀的地方是颤音里的低音部分,比较密的地方就是颤音里的高音部分了。我们图中演示的调制器的频率远远低于载波器的频率,所以这时声音听起来变成了颤音。那么当调制器的频率慢慢增加,接近、等于继而超过载波器的频率后会发生什么?为了清楚的说明这个问题,我们将没有经过调制的载波器的波形放大,放大到大约一个震动周期的八分之一,就是下图(Figure4)那样。

之后我们给这个载波器加上一个调制器,调制器使用几倍与载波器的频率,看下图(Figure5),载波器产生了大约7个弯曲,因为我们截取的是一个震动周期的八分之一,所以一个震动周期里产生了7X8大约60个左右的弯曲,这时反对声音就不是颤音了,那声音又变成了什么样呢?
无处不在的边带(Side Bands)
我们再返回来看式子5,里面的w2(调制器的频率)和a2(调制器的最大振幅)在起作用。John Chowning发现FM就像AM一样都会发生边带,也就是波形额外的部分,在输出信号的频率光谱上和载波器、调制器的频率完全没有关系。我们来看看FM是如何产生边带的。假设我们有一个正弦波的载波器,频率为Wc,还有一个频率为Wm的调制器,见上图(Figure6)。
与AM只发生两侧的边带(Wc+Wm)和(Wc-Wm)所不同的是,FM产生了一系列的边带,可以表示为式子6:
式子6:
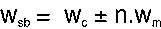
Wsb是FM产生的边带频率,实际上Wsb是一系列的数,因为n可以取任意的整数(0、1、2、3、4……)。每个边带平均分布在Wc(载波器频率)的两侧,分别是Wm(调制器频率)的任意整数倍。可以看到是调制器决定了边界的产生位置。理论上说n可以取无限的整数,也就是当调制器对一个载波器进行调制时会产生无穷级数的边带,但是在实际应用中不可能有能够产生无穷级数的设备,所以边带的值都被制造商限制在他们认为有意义的数里面了。下图(Figure7)形象的表示了边带的发生。
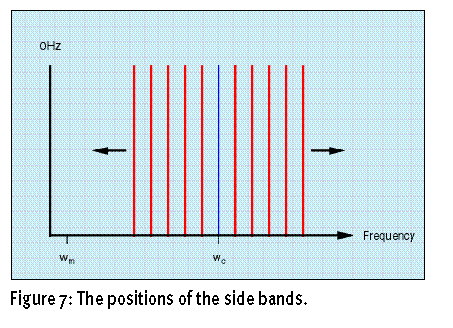
我们知道边带产生的位置了,那么边带的振幅又是怎么样的呢?取决于a2。我们引入一个新的概念--调值指数,或者直接称之为β值。(注意是拉丁字母β,念作贝塔)
我们将β定义为载波器扫过的频率(变化了的频率)与调制器的频率的比值,就是式子7:
式子7:
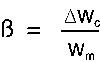
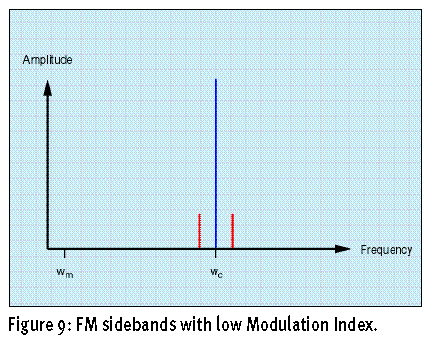
这个式子理解起来可能困难一些,要用到一些非常恐怖的数学公式,我们举个例子来说明一下。比如我们假定调值指数在0.1以下,边带的频率会非常接近载波器的频率,而且振幅较小,其他的边带都基本上没有振幅了,所以只剩下了一个边带。见上图(Figure9)。如果调制指数在5左右,那么会产生一系列的边带,而且频谱比较复杂,振幅有高有低。见下图(Figure10)。
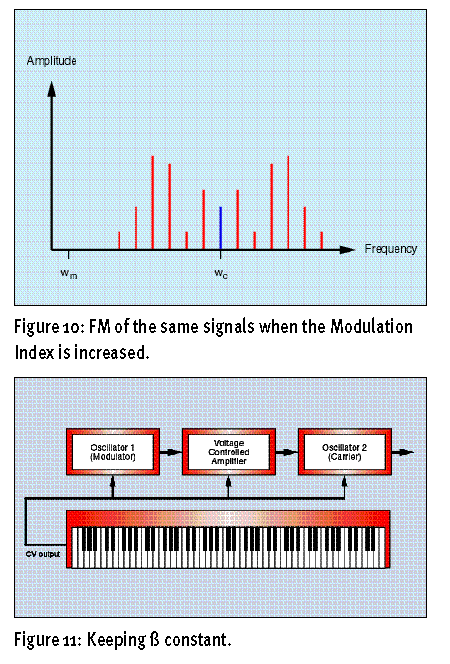
其实在调值指数为5时,边带不只6个,只是太多了画不过来。再仔细看上图(Figure10),没发现载波器的振幅(蓝线)变小了吗?哈哈真是奇怪,实际上取某个调值指数还能让载波器频率完全消失呢!
比如说你感觉Figure10里那个声音就是你想要的音色,你想像传统那样在键盘上从低音到高音弹出这个音色,这就取决于载波器和调制器在每个琴键上都平等的工作以便边带之间的谐波关系始终不变。但是让我们再回到式子7,式子7决定了一旦调制频率增加,那么调制指数就要下降。好比你由低到高弹一个八度,Wm增长了一倍,而β值变成了一半,那么声音可就全变了。为了避免光谱的改变,调制振幅也要成比例的增加--也变成以前的一倍,这样β值就会保持不变了。这实现起来并不难,用上图(Figure11)里的设备就可以实现。这个东西看起来似乎不能很准确的校准,但实际上完全没问题。
本文参考Sound On Sound的《Synth secrets--PART 12: AN INTRODUCTION TO FREQUENCY MODULATION》一文编译,有说的不对的翻译的不准确的望您指出
文章出处 midifan
转载文章请注明出自 Midifan.com




