解读FM合成器『7』--边带的振幅

解读FM合成器『7』--边带的振幅
OK经过前面的学习,我们对FM的合成方法基本上有了大致的了解了,但是你想在FM合成器(FM7或者是YAMAHA的DX系列)或是模块化的模拟合成器上弄出点好听的音色来,远比弄出一些奇怪的噪音要难的多。因为我们还不了解边带和载波器之间的关系,这一讲我要告诉你如何控制边带的振幅,这非常有趣,好了咱们开始吧!
我们已经知道FM信号里边带的频率是如何分布的了(前面讲过的),复习一下,是载波器加或减去整数倍的调制器频率,见式子1:
式子1:
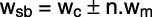
我们再引入一个新的概念,就是载波器频率与调制器频率的比值,载波器是Carrier,调制器是Modulator,所以我们简称为C:M比率。这个理解起来很简单,比如载波器是100Hz,调制器是200Hz,那么C:M比率就是1:2。
那么我们再看式子1,不管载波器的频率是多少,向上排列的边带就是C+M、C+2M、C+3M、C+4M……,向下排列的边带就是C-M、C-2M、C-3M、C-4M……。
假设C:M比率是1:1,那么也就是说载波器是1,向上的边带分别是2、3、4……,向下的边带就是0、-1、-2、-3、-4……。我们给一个具体的数值,比如载波器和调制器都是100Hz(C:M比率就是1:1),向上的边带就是200Hz、300Hz、400Hz……。这就是一个理想的100Hz的波形的谐波级数,换句话说1:1的C:M比率产生了一个谐波级数不管载波器的频率是多少。
但是向下的边带又是怎样的呢?应该是0Hz、-100Hz、-200Hz、-300Hz……。左右边带频率的位置都一样,而且声相相反,我们又知道异相信号会互相抵消,见下图。所以1:1的比率会造成100Hz与-100Hz抵消,200Hz与-200Hz抵消,一直抵消下去。那我们可怎么计算边带的振幅呢?
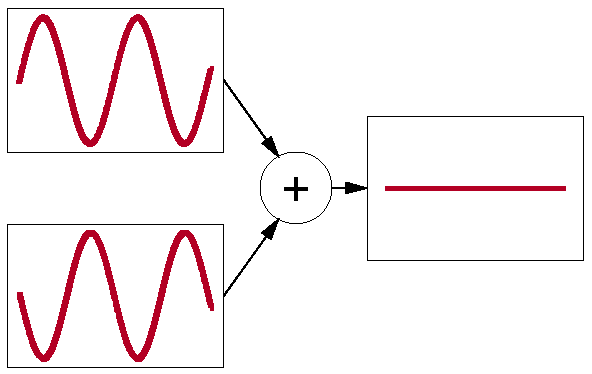
使用贝塞尔函数(Bessel Functions)!!
贝塞尔函数是特殊函数中应用最广泛的一种函数(就像我们熟知的π=3.1415926一样),他在理论物理研究、应用数学、大气科学以及无线电等工程领域都有广泛的应用(如果您想详细了解贝塞尔函数,建议您拜读奚定平写的《贝塞尔函数》一书),在FM领域贝塞尔函数也非常重要。如果咱们知道了调制指数,你就可以通过贝塞尔函数计算出任何频谱成分的振幅。
贝塞尔函数看起来有些难度,不过我还是希望你能坚持看完,最好不要跳过这些有趣(还是恐怖?)的数学知识。
我们定义载波器(简称为C)为你调制的信号的零点成分,那么C+M和C-M就是第一成分,C+2M和C-2M就是第二成分,C+3M和C-3M以此类推。现在我可以告诉你每对边带的振幅就可以用贝塞尔函数的n值计算,使用下面的式子2:
式子2:
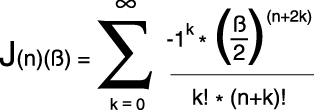
J(n)(β)就是当调制指数为β时的第n个贝塞尔函数,k是从0到正无穷的整数,k后面的感叹号表示k的阶乘(阶乘的意思就是假如k=3,那么k!=3X2X1=6,当k=5时,k!=5X4X3X2X1=120,注意0!≠0,而是=1),Σ表示k从0开始取值,一直加到k=正无穷时的值的和。别看他这么复杂,其实在你使用FM合成器时你无时无刻不在使用着这个式子,在你使用模拟合成器的交叉调制(Cross Modulation)时也是这个式子在起作用,实际上交叉调制就是频率调制的另一个名字。
我们还是使用贝塞尔函数计算振幅吧,假设调制指数β为0.1,那么要计算载波器零点成分的振幅,n就等于0,之后我们要分、分步计算,先把k作为0带入(见式子3),再计算第二部分的数值k就代为1(见式子4)。
式子3:
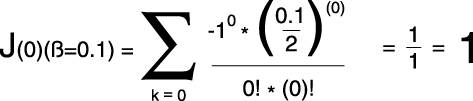
式子4:
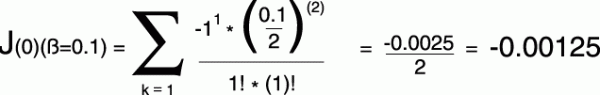
当然你还可以继续计算第三部分(k=2)第四部分(k=3)等的振幅,那么你会发现数值越来越小,可以说是非常小了,按理说我们要一直算到k等于正无穷时才可以,显然第三部分后面的微小数值我们都可以省略不算了。我们将第一部分、第二部分、第三部分相加,最后的结果就是调制指数为0.1时,载波器零点成分的振幅,振幅的数值近似等于1。
OK我们继续计算边带的振幅,这时n就要等于1了,调制指数不变依然是0.1,之后分步计算,先让k=0计算出一个数值,然后计算k=1、k=2……时的数值,最后将他们相加,就得出了C+M和C-M的边带。之后重复以上的步骤,只不过n变成了2,得出的是C+2M和C-2M的边带。一直增加n的数值计算下去。如果你有耐心你就算下去吧,直到地球爆炸……。
数学家不容易当吧,按照上面的做法真的是要累死,幸好我们有电脑啊!微软的Excel可以帮助我们计算不同调制指数下的贝塞尔函数。你可以看看下面几个不同调制指数下使用Excel制作出的图片,深蓝色是零点成分的振幅,绿色是周围边带的振幅。
调制指数为0时的振幅(自然没有边带产生):

调制指数为0.1时的振幅:
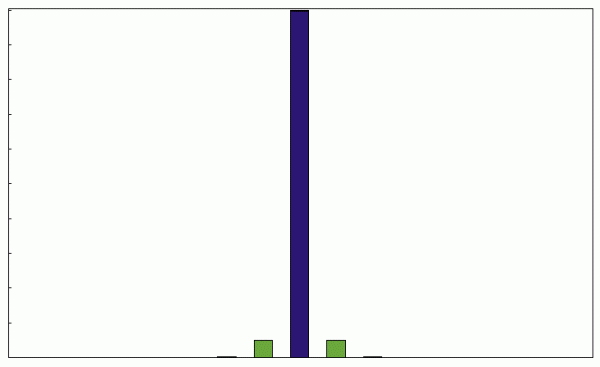
调制指数为0.5时的振幅:
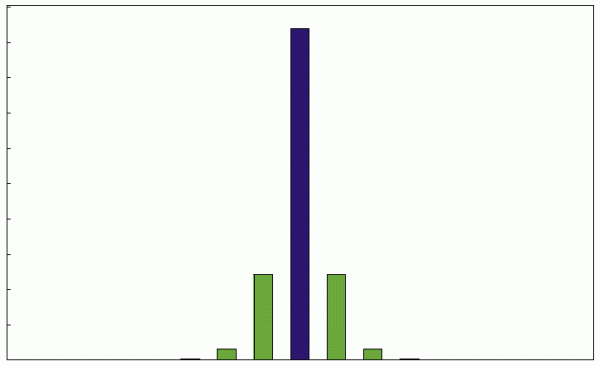
调制指数为1时的振幅:
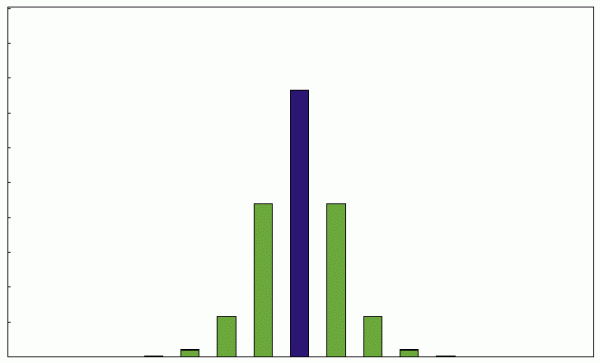
调制指数为2时的振幅:
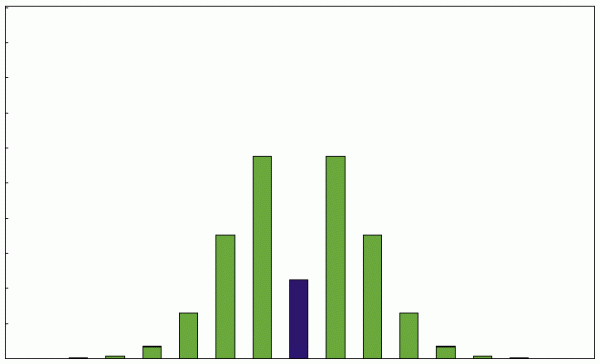
调制指数为5时的振幅:
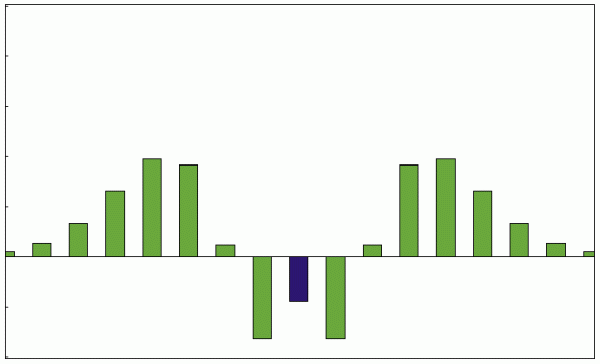
注意看上图,调制指数为5时,零点成分变成负的了,就是说那部分的声音反相了。
再看一眼上面在1:1的CM比下调制指数为1时的振幅。载波器的振幅,也就是零点成分基本上保留了他原始的高度。载波器右侧的振幅是2C、3C、4C和5C的谐波级数,它的左侧的第一个振幅是一个重要成分,这里是0Hz点(C是100Hz,M也是100Hz,所以C-M=0Hz,你可以把他当作是DC直流电点,因为在这一点震荡频率为零),在这个0点之后左侧分别是-C、-2C和-3C,那么他们就相当于反相位的C、2C和3C,请看下图(Figure8):
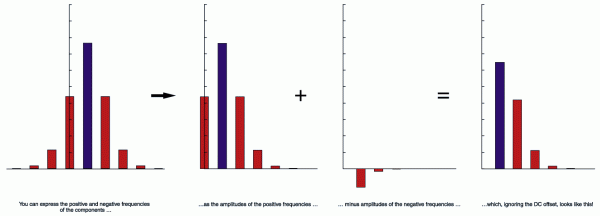
正反频率可以表示为 --> 正频率 + 反相位的负的负频率(或者说减去负频率) = 最后结果
如果我们忽略DC直流电(震荡频率为零的那个点),最后结果里的频谱包含了载波器的所有泛音。(只有1:1的CM比率是这样的),看最后结果的图像就像1/n谐波级数,他听起来就像锯齿波。
我们再来讨论当CM比率为1:2调制指数为1时的情况,这时载波器左右的边带分别就是C、3C、5C、7C……和-C、-3C、-5C、-7C……。他的图像和1:1时差不多,这时的声音听起来就像方波。
那么当CM比为1:3、1:4这些整数的时候呢?1:3时边带分别是4C、7C、10C……和-2C、-5C、-8C……,1:4时则是5C、9C、11C……和-3C、-7C、-11C……。声音听起来都近似于方波。
顺便解释一下上一讲里留的一个“扣子”,为什么在3600Hz的带宽下有24个特殊成分,信号里有10个右侧边带,1个载波器,1个可以忽略的左侧边带(DC直流电点)和12个左侧边带,一共就是24个了。
本文参考Sound On Sound的《Synth secrets--PART 13: MORE ON FREQUENCY MODULATION》一文编译,有说的不对的翻译的不准确的望您指出
文章出处 midifan
转载文章请注明出自 Midifan.com
-
2010-03-22
 匿名
think very much
匿名
think very much




