揭秘合成器(1):声音的构成
- 作者:Gordon Reid
- 编译:Rejor(@Evilsine)
- 出处:Sound On Sound
尽管这一系列文章的题目为「揭秘合成器」,我并不会真的在文章里揭示什么「秘密」。反之,我会为你介绍最常见的声音合成方法——减法合成的基础原理。然后告诉你如何将这些基础原理运用于特定合成器的使用过程中。
导语
尽管这一系列文章的题目为「揭秘合成器」,我并不会真的在文章里揭示什么「秘密」。反之,我会为你介绍最常见的声音合成方法——减法合成的基础原理。然后告诉你如何将这些基础原理运用于特定合成器的使用过程中。这一系列文章的目的是为了让你在使用以减法合成为原理的合成器的时候可以知道如何调制出自己心仪的音色,并且可以真正理解为什么调节哪些参数可以得到什么样的效果。事实上这一系列文章准确的标题其实应该是「为什么你在扭动合成器的某个旋钮的时候可以得到某种特定的效果...」,但说实话这实在不是个上口的名字,所以还是叫它「揭秘合成器」好了。
作为这一系列文章的第一篇,我会从一切的基础开始讲起:什么是减法合成?减法合成得名于其原理:通过减弱或者削除波形的一部分谐波从而创造出新的声音。使用这一原理你可以创造出简单的静态音色,也可以结合合成器的滤波器(filters)、包络发生器(envelope generators)以及调制器(modulators)等工具创造出随时间而变化的动态声音。听到这里你可能已经摸不到头脑了:谐波是什么?波形又是什么?这些概念是从哪来的?它们之间又有什么关系?
为了回答这些基础问题,我们需要乘坐时光机回到过去,回到那个没有物理建模、没有采样器、没有模拟复音合成器、甚至没有单音合成器的古老年代...
历史
事实上,我们需要穿梭回 2500 年前,从著名的古希腊哲学家、数学家毕达哥拉斯开始说起。
毕达哥拉斯有一项鲜为人知的发现:如果用同样的力度拨动两根材质相同的绳子,当两根绳子的长度比例处于整数倍关系时发出的合音会比较悦耳。
打比方说,如果一根绳子的长度是另外一根绳子的一半(1:2 的关系)的话,拨动两根绳子产生的合音会很悦耳。如果长度关系是 2:3 的话效果也会不错。
但为什么两根绳子长度为整数关系时更悦耳呢?为了回答这一问题,让我们先假设有一根绳子,它的两端是固定起来的,中间的部分可以任意震动,该绳静止时的状态如图 1 所示。
现在拨动一下这根绳子正中间的位置,振动时的状态如图 2:
上面列举的是一个「驻波」的例子。振动过程中,绳子中点的位置会上下反复移动。理想状态下,以时间为横轴,绳子移动为纵轴,将绳子的震动过程以图案形式记录下来就得到了正弦波(sine wave)(图 3),我们将这一类图案称为「波形(waveform)」。
波形完成一个周期的频率被称之为波形的基本频率(fundamental frequency),在本例中也就是这根绳子震动的基本频率。
虽然绳子的两头被固定,震动的方式和速度因此会受到限制,然而绳子被拨动这一过程中,并非只会生成一个基本频率。想象把你的手指放在绳子的正中间(整根绳子还是可以正常震动),接着任意拨动绳子的左半边或者右半边,这样就得到了一个波长为原始长度 1/2 的驻波(如图 4 所示)。
同理,如果把手指放在绳子长度 1/3 的位置就可以得到一个波长为原始长度 1/3 的驻波(如图 5)。
以此类推,只要处于整数倍关系,驻波就可以被产生。这些驻波叫做基础频率的谐波(harmonics)。
如果你对驻波的数学原理有研究,你就会知道驻波可以被认为是在同一根绳子上的两个相反方向「行进」中的波形合成起来构成的(别问我为什么,否则这篇文章就永远也写不完了)。通过这一原理不难可以得到这一结论:如果将波长减半,波形的频率就会翻番,变成原始频率的两倍。类似地,如果将波长缩减至原始波长的三分之一,频率将升高至原始频率的三倍;四分之一则会升高至四倍,以此类推...之所以倍数必须是整数是因为如果你想引入一个非整数倍的频率变化那么绳子就不可以处于其零点位置,也就是绳子的两端(不满一个震动周期),然而绳子的两端是固定起来的,所以这种情况不可能存在。
当然,不光只有震荡的绳子遵循这一规则。以一个立方体房间中的空气为例,为了不把这一假设搞得过于复杂,我们暂时不考虑家具等其他可能对条件产生影响的元素,空气可以在房间中除了墙体、地板和天花板之外的任意位置自由振动。换句话说,房间中空气的震动方式和绳子的震动方式是完全一致的。房间本身也具备谐波频率,这也就是普通房间会产生「共振」的原因。管风琴也正是运用了这一原理发声,管风琴的音管也就是简单的谐波振荡器。
震荡产生的第一谐波(基础频率,记作 f)就是当你听到震荡产生的声音的时候感知的音高。第二谐波(也被称为第一「泛音(overtone)」)的波长为基频的一半,因此频率为基频的两倍。如果单独聆听这一频率,我们会感知到比基频高正好一个八度的音高。
第三谐波的频率为 3f(比基本高一个半八度,纯五度关系),第四谐波的频率为 4f,比基频高两个八度。接下来的三个谐波与第四谐波处于同一个八度,第八谐波比基频高三个八度,以此类推...
通过这一规律我们就可以理解毕达哥拉斯的观察。当两根绳子长度成 1:2 关系时,较短的那根绳子被拨动时产生的基频与较长的那根的第二谐波频率正好相等。当两根绳子长度成 2:3 关系时,较长的那根绳子的第三谐波与较短的那根的第二谐波频率相等。换句话说,如果两根绳子的谐波构成彼此相似的话,我们听到的声音就会比较「悦耳」。
考虑这一点:当你拨动绳子的时候,你并不只会听到单独的一个谐波。如此纯净的频率需要及其精准的条件才可以产生,在自然界中几乎无法达成。因此自然界中的所有声音几乎都是由一系列不同量度的谐波构成的。这一谐波构成决定声音在任意时间片刻的波形,因为大量谐波的存在,这类波形要比图 3 中展示的正弦波复杂得多。把吉他采样或者人声录音放在波形编辑器中你就可以看到真实的波形的复杂程度。
声音的分析或者合成也因为这一点而极其困难,几乎无法实现。但是一位名叫 Jean Baptiste Joseph Fourier 的数学家发现任何周期运动,无论多么复杂,都可以通过一系列计算将其分解为谐波构成。为了纪念这位数学家,这一程序被命名为傅立叶分析。除此之外,利用傅立叶分析还可以反推出一系列谐波的波形。
等等...波形决定谐波,谐波也可以决定波形?显然,谐波与波形只是表达同一个概念的两种不同方式。关键在于:音色取决于其谐波的数量与幅度;通过给定的一系列谐波可以合成波形。所以当你看到合成器上的「方波(square)」或者「锯齿波(sawtooth)」等波形,实际上是在说「这一设置可以生成一系列幅度为 x、y 与 z 的谐波」。
让我们把这一认识运用于合成器上。观察图 6 中的波形,这是一个理想的「锯齿波」波形,其形状与锯齿相似而因此得名。拨动绳子的时候绝对无法产生如此简单的波形,但是几乎每一台合成器都可以产生类似的锯齿波。
这一波形由一系列处于下列简单关系的谐波构成:
每个谐波均存在,且第 n 谐波的幅度等于基频幅度的 n 分之一。
虽然这一关系听起来已经不是很简单了,但相信我,还有其他波形比锯齿波复杂得多。总之,图 7 展示的是锯齿波的前十个谐波,可以看到谐波的频率越高振幅就越小。
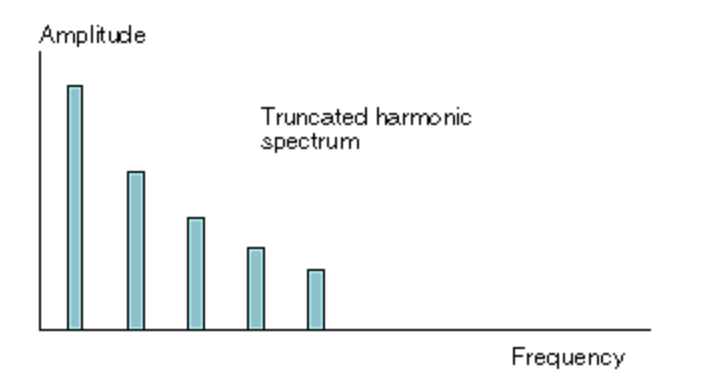
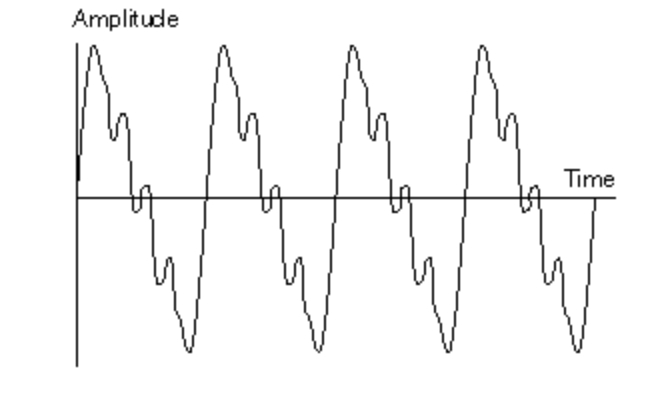
但如果把这一系列的谐波截断会怎么样?比方说,(使用滤波器)把除了前五个谐波之外的其他高频谐波全部移除。图 8 展示的是经过这一移除之后该波形的频谱,图 9 展示的是其对应的波形。
可以看到,新的波形与锯齿波的形状相比有所不同。这一波形的声音也和锯齿波有所差别。但是这两个波形的不同之处只是你将锯齿波的高频谐波过滤掉了,只剩了前几个谐波。换句话说,你使用了一个「滤波器」「减去」了一部分谐波,从而创造了一个新的波形,也因此合成了一个新的声音。
欢迎来到减法合成的世界!
文章出处 https://www.soundonsound.com/techniques/synth-secrets-all-63-parts-sound-on-sound
转载文章请注明出自 Midifan.com
-
2022-09-10
 匿名
太牛了!
匿名
太牛了! -
2021-06-20
 NeonSounds
谢谢这个系列一定要更下去呀!!
NeonSounds
谢谢这个系列一定要更下去呀!! -
2020-11-03
 匿名
太棒了,谢谢!
匿名
太棒了,谢谢! -
2020-07-27
 匿名
牛逼,学到了
匿名
牛逼,学到了 -
2019-05-26
 匿名
牛逼!求继续更新
匿名
牛逼!求继续更新 -
2019-05-13
 匿名
讲得好啊!
匿名
讲得好啊!